警告: 目前在草稿阶段, 请忽略此文章

神经网络原理与数学基础

前言

这是一个原理讲解, 旨在帮助读者理解神经网络的基本原理和数学基础。

作者声明

我本人是一名初中生, 因此我会尽量使用简单的语言来解释复杂的概念。本文面向初学者, 我希望像我一样的初中生都能看懂这篇文章, 并理解神经网络的原理。

由于我是初中生, 所以可能会有一些错误, 如果你发现了错误, 请在评论区指出来, 我会及时更正。我本人全靠自学, 所以可能会有一些不准确或认知偏激的地方。我发文章的目的之一就是纠正我的错误, 希望大家能帮我一起完善这篇文章。

神经网络基本流程

核心概念

1. 数据集:

   • 模型会拟合数据集
   • 数据集是模型训练的基础
   • 包含输入数据和对应的真实结果(标签)
   • 可以简单理解为学习资料

2. 模型:

   • 本质是一个函数
   • 接受输入数据, 经过计算后输出结果
   • 训练过程就是调整函数参数

3. 训练流程:

   • 前向传播: 输入数据经过计算得到输出结果
   • 损失函数: 计算输出结果与真实结果的差距
   • 反向传播: 计算参数梯度
   • 优化器: 根据梯度更新参数

深度学习数学基础入门

如果你想认真学习深度学习，数学基础是不可或缺的。这里列举一些必要的概念，帮助你打好基础。如果你已经有数学基础，可以跳过这些内容。

概念:
1.维度可以简单理解为数字的数量,例如768维度的向量指的就是有768个数字的向量.
2.函数可以理解为一种映射关系,即把输入映射为输出.
3.张量就是数组, 2维张量就是嵌套了2个数组的数组, 例如[[1,2],[2,3]]就是一个2维张量

1. 什么是函数？

函数可以理解为一种“映射关系”，即把输入映射为输出。

例子：

• f(x) = x + 1
• y = x + 1

一般情况下，f(x) = x + 1 可以理解为 y = x + 1，这两个实际上差不多，只是写法不同。函数强调的是输入和输出的对应关系。

扩展知识（可选）：

• 定义域：允许输入的集合
• 值域：可能输出到哪
• 图像：所有 (x, f(x)) 构成的点的集合

2. 什么是极限？

极限用来探索当 x 趋近某个数值时，函数的输出会是什么。

例子：
f(x) = \dfrac{1}{x}

我们可以求不同的 x 值对应的 f(x):

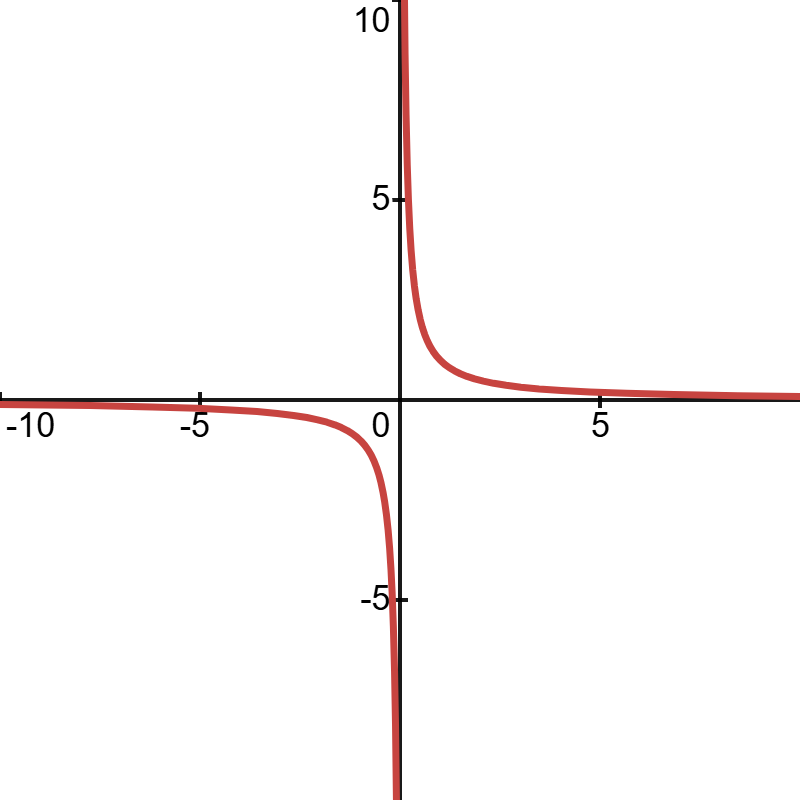
因此我们会发现：

当 x 从右侧越来越接近 0 时，f(x) 会越来越大，趋向于 +\infty
当 x 从左侧越来越接近 0 时，f(x) 会越来越小，趋向于 -\infty

因此我们可以说：

当 x \to 0^+ 时，f(x) \to +\infty
读作：“当 x 趋于 0 的右极限时，f(x) 趋于正无穷”

当 x \to 0^- 时，f(x) \to -\infty
读作：“当 x 趋于 0 的左极限时，f(x) 趋于负无穷”

由于左右极限不相等，双侧极限不存在。

3. 什么是导数？

导数可以理解为瞬时变化率，同时他在图像上还是切线的斜率。

定义公式：

f'(x) = \lim_{h\to 0} \frac{f(x+h) - f(x)}{h}

例子:
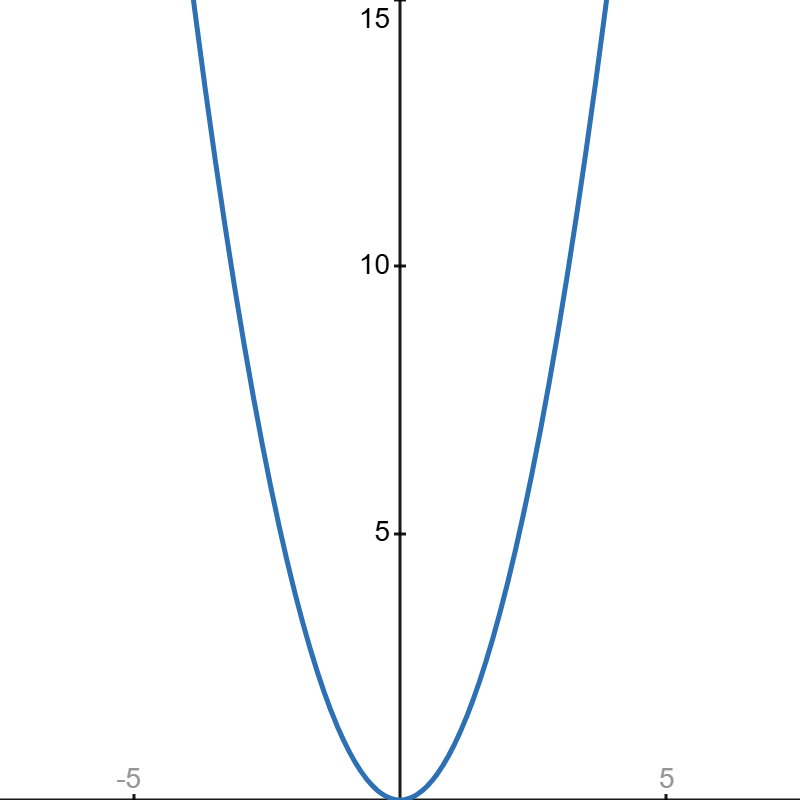
假设路程函数为 f(x) = x^2，其中 x 轴表示时间，y 轴表示路程。

\begin{aligned} f'(x) &= \lim_{h\to 0} \frac{(x+h)^2 - x^2}{h} \\ &= \lim_{h\to 0} \frac{2xh + h^2}{h} \\ &= \lim_{h\to 0} (2x + h) \\ &= 2x \end{aligned}

因此该函数的导函数是 f'(x) = 2x, 那么每个时刻的瞬时速度为：

• x = 1 → 速度 = 2
• x = 2 → 速度 = 4
• x = 3 → 速度 = 6

4. 什么是偏导数？

偏导数是多变量函数在某一个变量方向上的变化率。
你可以简单理解为就是“对其他变量保持不变，只考虑一个变量对函数带来的变化”。

例子：

f(x, y) = x^2 + y^2

• 对 x 的偏导：\dfrac{\partial f}{\partial x} = 2x
• 对 y 的偏导：\dfrac{\partial f}{\partial y} = 2y

在深度学习中，神经网络的参数通常是多维(有许多参数)的，所以偏导数非常重要。

梯度：收集所有偏导组成的向量，记作

\nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)

5. 什么是链式求导？

链式法则用于求复合函数的导数。

例子：
f(x) = (3x + 2)^2

可以被拆分为: f(u) = u^2, 其中 u = 3x + 2

• 外层函数 u^2 → 导数 2u
• 内层函数 3x + 2 → 导数 3
• 链式法则：

f'(x) = 2(3x + 2) \cdot 3 = 6(3x + 2)

链式求导是反向传播算法的数学基础。
因为深度学习的网络层数多, 通过链式法则可以快速计算每层网络的偏导数(梯度).
例如一个3层网络可能长这样:
f(x) = relu(w(relu(wx+b))+b)
这时就需要用到链式法则来计算每一层的梯度。

6. 什么是矩阵？

矩阵是按行列排列的数字表，可以表示数据或线性变换。

矩阵乘法规则：

C[i, j] = \sum_k A[i, k] \cdot B[k, j]

即 A 的第 i 行与 B 的第 j 列对应元素相乘再求和。

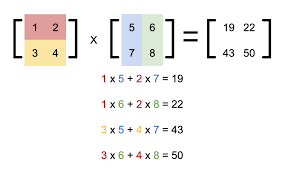
例子：
A = \begin{bmatrix} 5 & 6 \end{bmatrix}（1 \times 2 矩阵）
B = \begin{bmatrix} 1 \\ 2 \end{bmatrix}（2 \times 1 矩阵）

计算：

C = \begin{bmatrix} 5 & 6 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} 17 \end{bmatrix}

7. 关键词速览（最好知道的）

这些内容不是必须马上掌握的，但学会后会让你更容易理解深度学习。

• 函数、定义域、值域、图像
• 极限、左极限、右极限、连续
• 导数、切线斜率、求导法则
• 偏导、梯度、链式法则
• 向量、点积、范数、余弦相似度
• 矩阵、形状、转置、单位矩阵、矩阵乘法
• 指数、对数、Softmax、交叉熵
• 损失函数、学习率、梯度下降

接下来，你已经有了基础数学知识，就可以直接进入深度学习的基础概念，比如训练一个简单的Linear（全连接）层，看看数学是如何在模型训练中发挥作用的。

什么是层?

基本概念

我们举个例子-线性层(Linear Layer)是神经网络中最基础的组成部分, 类似编程中的 “Hello World”。它的主要作用是对输入数据进行线性变换。

数学表达式

Linear(x) = w * x + b

其中:

• y: 输出结果
• w: 权重矩阵
• x: 输入数据
• b: 偏置项

理解线性层

两种解释线性层的定义:

1. 线性函数角度:

   • 类似于 f(x) = kx + b
   • w 是可学习的斜率
   • b 是可学习的偏置

2. 模式识别角度:

   • 权重表示特征敏感度
   • 偏置控制"感兴趣"阈值

激活函数

激活函数是为了解决线性层无法解决非线性问题,而且在不引入激活函数的情况下,堆叠再多的线性层也无法增加模型的表达能力, 因为不过多少层的线性层都可以化简为单层线性层。
激活函数对线性变换结果进行非线性变换, 使模型能学习更复杂的特征。常见的激活函数包括:

ReLU (修正线性单元)

• 定义: f(x) = max(0, x)
• 特点: 计算简单, 收敛快速

Sigmoid (逻辑函数)

• 定义: f(x) = 1/(1 + e^(-x))
• 特点: 输出范围 [0,1], 适用于二分类
• 缺点: 可能导致梯度消失, 梯度消失发生的原因就是因为随着层数越来越靠前,导数也越来越接近0

介绍完这些后,我们就迎来了深度学习最重要的概念–反向传播

反向传播就